publications

2025

1. 

   A Mixed Model Approach for Estimating Regional Functional Connectivity from Voxel-level BOLD Signals

   Ruobin Liu, Chao Zhang, Chau Tran, Sophie Achard, Wendy Meiring, and Alexander Petersen

   submitted, 2025

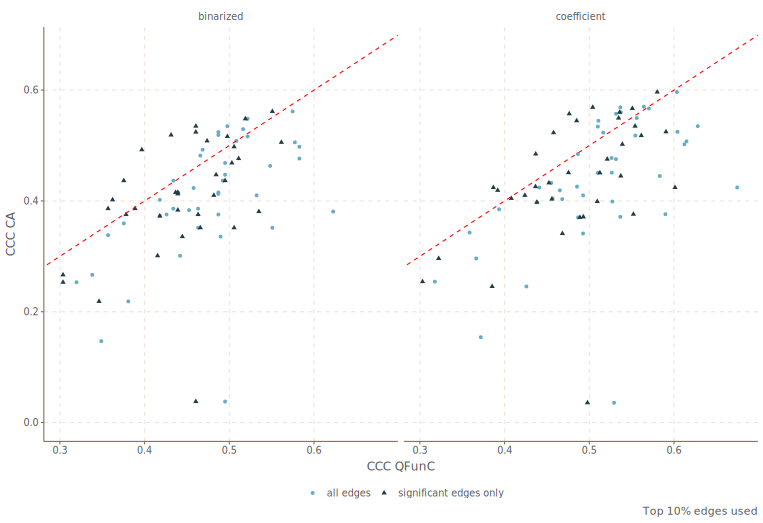
   Abs arXiv

   Resting-state brain functional connectivity quantifies the synchrony between activity patterns of different brain regions. In functional magnetic resonance imaging (fMRI), each region comprises a set of spatially contiguous voxels at which blood-oxygen-level-dependent signals are acquired. The ubiquitous Correlation of Averages (CA) estimator, and other similar metrics, are computed from spatially aggregated signals within each region, and remain the quantifications of inter-regional connectivity most used by neuroscientists despite their bias that stems from intra-regional correlation and measurement error. We leverage the framework of linear mixed-effects models to isolate different sources of variability in the voxel-level signals, including both inter-regional and intra-regional correlation and measurement error. A novel computational pipeline, focused on subject-level inter-regional correlation parameters of interest, is developed to address the challenges of applying maximum (or restricted maximum) likelihood estimation to such structured, high-dimensional spatiotemporal data. Simulation results demonstrate the reliability of correlation estimates and their large sample standard error approximations, and their superiority relative to CA. The proposed method is applied to two public fMRI data sets. First, we analyze scans of a dead rat to assess false positive performance when connectivity is absent. Second, individual human brain networks are constructed for subjects from a Human Connectome Project test-retest database. Concordance between inter-regional correlation estimates for test-retest scans of the same subject are shown to be higher for the proposed method relative to CA.

2. 

   Estimation of the Error Structure in Multivariate Response Linear Regression Models

   Ruobin Liu and Guo Yu

   WIREs Computational Statistics, 2025

   e70021 EOCS-730.R1

   Abs DOI HTML

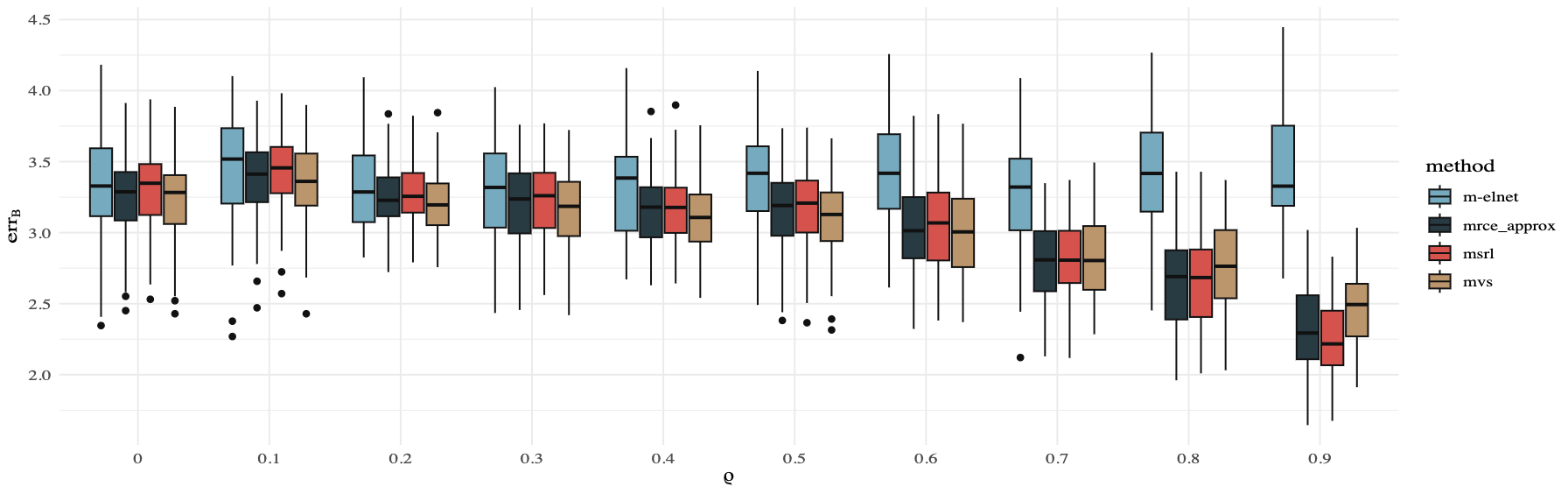
   Multivariate response linear regression model considers how a set of covariates affects multiple responses. In contrast to separately running univariate regression for each response, multivariate response regression can better estimate the coefficient matrix by exploiting shared information among the responses. A key to effectively borrowing strength across different responses is to estimate and utilize the structure among random errors in responses. Moreover, certain applications seek to understand the interrelationships of the responses, which are directly encoded in the error structure. These observations call for the development of methods for estimating the error structure in multivariate response linear regression models. This article aims at providing a review of recent progress in this challenging and important problem. We also provide simulation studies demonstrating the empirical performance of recently developed methods for error structure estimation, as well as the benefit by exploiting these estimates for regression coefficients estimation.

2024

1. 

   A convex formulation of covariate-adjusted Gaussian graphical models via natural parametrization

   Ruobin Liu and Guo Yu

   in preparation, 2024

   Abs arXiv

   Gaussian graphical models (GGMs) are widely used for recovering the conditional independence structure among random variables. Recently, several key advances have been made to exploit an additional set of variables for better estimating the GGMs of the variables of interest. For example, in co-expression quantitative trait locus (eQTL) studies, both the mean expression level of genes as well as their pairwise conditional independence structure may be adjusted by genetic variants local to those genes. Existing methods to estimate covariate-adjusted GGMs either allow only the mean to depend on covariates or suffer from poor scaling assumptions due to the inherent non-convexity of simultaneously estimating the mean and precision matrix. In this paper, we propose a convex formulation that jointly estimates the covariate-adjusted mean and precision matrix by utilizing the natural parametrization of the multivariate Gaussian likelihood. This convexity yields theoretically better performance as the sparsity and dimension of the covariates grow large relative to the number of samples. We verify our theoretical results with numerical simulations and perform a reanalysis of an eQTL study of glioblastoma multiforme (GBM), an aggressive form of brain cancer.

2. 

   Deep residual networks for crystallography trained on synthetic data

   Derek Mendez, James M. Holton, Artem Y. Lyubimov, Sabine Hollatz, Irimpan I. Mathews, Aleksander Cichosz, Vardan Martirosyan, Teo Zeng, Ryan Stofer, Ruobin Liu, Jinhu Song, Scott McPhillips, Mike Soltis, and Aina E. Cohen

   Acta Crystallographica Section D, Jan 2024

   Abs DOI HTML

   The use of artificial intelligence to process diffraction images is challenged by the need to assemble large and precisely designed training data sets. To address this, a codebase called \it Resonet was developed for synthesizing diffraction data and training residual neural networks on these data. Here, two per-pattern capabilities of \it Resonet are demonstrated: (i) interpretation of crystal resolution and (ii) identification of overlapping lattices. \it Resonet was tested across a compilation of diffraction images from synchrotron experiments and X-ray free-electron laser experiments. Crucially, these models readily execute on graphics processing units and can thus significantly outperform conventional algorithms. While \it Resonet is currently utilized to provide real-time feedback for macromolecular crystallography users at the Stanford Synchrotron Radiation Lightsource, its simple Python-based interface makes it easy to embed in other processing frameworks. This work highlights the utility of physics-based simulation for training deep neural networks and lays the groundwork for the development of additional models to enhance diffraction collection and analysis.